
摘要:在高中物理必修教材《万有引力》一章中,给出了万有引力常数G的数值和测量方法。由于实验条件的限制,无法用实验室的仪器测出引力常数G,这使得测量方法停留纸面上。在研究性学习过程中,我们遇到了弹性空间问题,该问题的情景与引力空间相似。我们发现“常数G”可以通过常规的实验手段进行测量,并且在探究的过程中,要对弹性空间建立实验模型并定义相关的物理参量。在猜想、定义、分析和测量的基础上,我们计算出了“常数G”的平均值。下面介绍探究弹性空间的过程和方法。
关键词:弹性空间;猜想;定义;分析;测量
0、弹性空间
在动力学中常常用舒展的水平薄膜上的大球之间的相互作用来说明万有引力。试进一步的研究这个系统,尽可能定义并测量在这个“空间”中的“引力常数”(选自2014IYPT)。
1、实验设计
 如图1所示,在水平放置的玻璃缸边缘紧紧地蒙上一层PE保鲜膜,使保鲜膜的表面平整而没有褶皱,在保鲜膜的中央放上一个不锈钢大球,观察发现,膜的表面下陷。用弹簧枪发射一个光滑的不锈钢小球,使其获得一定的初速度并沿玻璃缸边缘切线方向运动,观察两个小球以后的运动情况。
如图1所示,在水平放置的玻璃缸边缘紧紧地蒙上一层PE保鲜膜,使保鲜膜的表面平整而没有褶皱,在保鲜膜的中央放上一个不锈钢大球,观察发现,膜的表面下陷。用弹簧枪发射一个光滑的不锈钢小球,使其获得一定的初速度并沿玻璃缸边缘切线方向运动,观察两个小球以后的运动情况。
实验中有以下几点需要说明:
(1)在玻璃缸中放入棉布是为了防止球砸坏水缸。
(2)在玻璃缸上蒙一层保鲜膜后,缸内气体不容易逸出,阻碍了薄膜的形变。在玻璃缸边缘密封处,安放塑料吸管,让玻璃缸内的气体与外界相通,使薄膜正常形变。
(3)保鲜膜表面带有大量电荷,把保鲜膜平展开,放置在背阴、通风处数日,使保鲜膜表面的净电荷减少。
2、探究1:弹性空间的受力特征
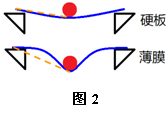 2.1 薄膜的形变
2.1 薄膜的形变
放上大球后薄膜绷紧,产生形变, 如图2所示,硬板的形变是凹形,薄膜的形变是凸形。
2.2 小球运动的受力分析
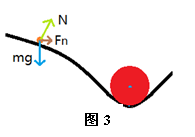 若小球在水平面内做匀速圆周运动,在不考虑阻力的情况下,小球的受力如图3所示,重力mg和支持力N的合力Fn提供了小球在水平面内做匀速圆周运动的向心力,其向心力的大小为
若小球在水平面内做匀速圆周运动,在不考虑阻力的情况下,小球的受力如图3所示,重力mg和支持力N的合力Fn提供了小球在水平面内做匀速圆周运动的向心力,其向心力的大小为
Fn=mgtanθ。
事实上,薄膜和小球间的滚动摩擦不可忽略,小球因摩擦而损失能量后,必定会做缓慢的近心运动。小球运动的每一圈内,由于速度的大小变化较小,可以近似地认为小球在该圈内做匀速圆周运动。
3、探究2:弹性空间的运动学特征
按上述的实验装置,给小球不同的初速度进行多次实验,观察到的实验现象如下:
(1)在膜的边缘沿切线方向以某一速度υ释放小球,可以观察到小球运动一周的轨迹是正圆;
(2)在同一位置,沿同一切线方向释放小球,初速度小于υ,则小球运动一周的轨迹是椭圆,小球接近大球时速度变快,远离大球时速度变慢;
(3)在同一位置,沿同一切线方向释放小球,初速度大于υ,则小球飞离薄膜,此时小球的轨迹为抛物线或双曲线;
(4)小球运动几圈之后便会撞到大球上,这表明小球和薄膜之间存在着滚动摩擦;
(5)实验中,大球的质量约是小球的65倍(m大球=500.42g,m小球=7.73g),小球接近大球时,大球也有明显的运动。使用两个质量相近的球进行实验时,可以观察到两球相互绕动。
4、探究3:“空间”对比分析
表1
| 特征 空间 | 动力特征
| 阻力特征 | 运动特征 | 几何焦点 |
| 地球空间 | 地球引力
| 较小 |
近似匀速圆周运动、椭圆运动抛物线运动或双曲线运动
| 地球 |
| 太阳系空间 | 太阳引力 | 较小 | 太阳 | |
| 宇宙空间 | 万有引力 | 较小 | “宇宙中心” | |
| 弹性空间 | 弹力、重力的合力 | 较大 | 质量较大的球 |
结论:“弹性空间”和“引力空间”的动力学和运动学特征基本相似,弹性空间所受的阻力较大。
5、探究4: 开普勒第三定律中的常数k
5.1 猜想
既然弹性空间与引力空间基本相似,那么开普勒第三定律在弹性空间中仍然适用。猜想: 在弹性空间中,小球绕大球做椭圆运动时,其半长轴的三次方跟公转周期的二次方的比值为常数。
5.2 开普勒第三定律中的常数
由开普勒第三定律,小球绕大球做椭圆运动时,其轨迹半径的三次方与周期的二次方的比值为常数k。即
![]()
在测量过程中,测量小球做匀速圆周运动的半径和周期。
5.3 匀速圆周运动的半径
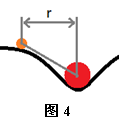
如图4所示,两球心间的距离在水平方向上的投影为小球做匀速圆周运动的轨迹半径,记为 r。
5.4 实验数据
实验中使用佳能600D数码相机,运用暴风影音软件,测量数据记录如表2所示。
表2
| 实验次数 | 轨迹半径r/m | 周期T/s | 比值k/m3·s-2 |
| 1 | 0.1135 | 1.954 | 3.83×10-4 |
| 2 | 0.1 | 1.704 | 3.44×10-4 |
| 3 | 0.0914 | 1.582 | 3.05×10-4 |
| 4 | 0.0814 | 1.364 | 2.90×10-4 |
| 5 | 0.0764 | 1.32 | 2.56×10-4 |
| 6 | 0.0693 | 1.141 | 2.56×10-4 |
| 7 | 0.065 | 1.113 | 2.22×10-4 |
| 8 | 0.0564 | 0.96 | 1.95×10-4 |
| 9 | 0.0529 | 0.882 | 1.90×10-4 |
| 10 | 0.0486 | 0.819 | 1.71×10-4 |
5.5 结论
取上述十组数据的平均值, k的平均值为2.61×10-4 m3·s-2,该实验在误差允许的范围内验证了猜想。
6、探究4:弹性空间中“引力常数”的测量
 6.1 “引力”的定义
6.1 “引力”的定义
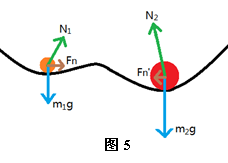
如图5所示,小球重力和所受支持力的合力为大球对小球作用力,记为![]() 。大球重力和所受支持力的合力为小球对大球作用力,记为
。大球重力和所受支持力的合力为小球对大球作用力,记为![]() 。称
。称![]() 和
和![]() 是两球间的相互“引力”,记为
是两球间的相互“引力”,记为![]() 。
。
6.2 弹性空间中“万有引力定律”的推导
小球做匀速圆周运动,线速度与周期的关系为
![]()
由向心力公式可得
![]()
由上述两式可推出
![]()
结合
![]()
得到
![]()
其中k和π都是常量,于是可知
![]()
由于两球相互绕动,若以小球为参考系来研究大球的运动,同样可以推出
![]()
根据牛顿第三定律应有
![]()
由此可以得出:两球间的“引力”与两球质量的乘积成正比,与两球距离的平方成反比。即
![]()
可以改写成等式,即
![]()
其中:G便是弹性空间中的“引力常数”。
7、探究5:“引力常数”的测量
由向心力公式得
![]()
考虑到
![]()
因此,“引力常数”的表达式为
![]()
把数据k=2.61×10-4m3/s2 、M=0.50042kg代入上式即可得到得到
G=2.06×10-2 N·m2/kg2
8、展望
上述探究过程中,由于薄膜和两球间之间存在滚动摩擦,使得弹性空间和引力空间存在一定的差异,这有待于进一步减小摩擦来提高测量的精度,但这并不妨碍对弹性空间中“引力常数”的粗略测定和探究方法的应用。探究过程中的摩擦因素,好比“一朵小小的乌云”,等待“一缕阳光”去拨开照亮。
说明:
(1)本论文系江苏省中小学教学研究室立项课题“高中物理教学过程中原创力的认
识和培护问题研究”的研究成果之一,课题编号:jk9-2006。
(2)本成果曾参加首届江苏省高中物理学科研究性学习成果汇报展评活动(JSYPT2013)而荣获银奖。