
三角函数恒等变换
二倍角的三角函数——第一课时(二倍角公式的推导,求值)
例1 求下列各式的值:
(1) sin15°cos15°; (2) cos4![]() -sin4
-sin4![]() ;
;
变式:利用二倍角公式,求cos![]() cos
cos![]() cos
cos![]() cos
cos![]() 的值.
的值.
例2 已知sina=![]() ,a∈(
,a∈(![]() ,π),求sin2a,cos2a,tan2a的值.
,π),求sin2a,cos2a,tan2a的值.
例3 若tanq=3,求sin2q的值.
例4 已知sin(![]() +α)=
+α)=![]() ,求sin2α.
,求sin2α.
二倍角的三角函数——第二课时(二倍角公式变形,化简、证明)
例1化简![]() -
-![]() ,其中a∈(
,其中a∈(![]() ,
,![]() ).
).
例2化简![]() ,其中a∈(
,其中a∈(![]() ,2π).
,2π).
例3 求证![]() =tanθ.
=tanθ.
例4 求函数y=cos2x+cosxsinx的值域![]()
练习:已知函数f (x)=sin2x+![]() sinxcosx+2cos2x,x
sinxcosx+2cos2x,x![]() R.
R.
(1) 求函数f(x)的最小正周期和单调增区间;
(2) 求函数f(x)的最大值和最小值;
(3) 求函数f(x)的对称轴和对称中心;
(4) 用五点法作出函数f(x)在一个周期上的图象;
(5) 函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
例5 化简:sin2(α-![]() )+sin2(α+
)+sin2(α+![]() )-sin2α.
)-sin2α.
 二倍角的三角函数——第三课时(三角关系式的综合应用)
二倍角的三角函数——第三课时(三角关系式的综合应用)
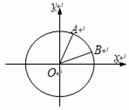
例1 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角a,b,它们的终边分别交单位圆于A,B两点.已知A,B两点的横坐标分别是![]() ,
,![]() .
.
(1)求tan(a+b)的值; (2)求a+2b的值.
例2 已知向量a=(3sin α,cos α),b=(2sin α,5sin α-4cos α), α∈![]() ,且a⊥b.
,且a⊥b.
(1)求tan α的值;(2)求cos![]() 的值.
的值.
练习:已知a=(2cos x,1),b=(![]() sin x+cos x,-1),函数f(x)=a·b.
sin x+cos x,-1),函数f(x)=a·b.
(1) 求f(x)在区间[0,![]() ]上的最大值和最小值;
]上的最大值和最小值;
(2) 若f(x0)=![]() ,x0∈[
,x0∈[![]() ,
,![]() ],求cos2x0的值;
],求cos2x0的值;
(3) 若函数y=f(ωx)在区间(![]() ,
,![]() )上是单调递增函数,求正数ω的取值范围.
)上是单调递增函数,求正数ω的取值范围.
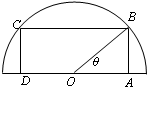 例3 在半圆形钢板上截取一块矩形材料,怎样截取能使这个矩形的面积最大?
例3 在半圆形钢板上截取一块矩形材料,怎样截取能使这个矩形的面积最大?
分析:只要矩形的的一个顶点确定了,矩形就确定了,那如何
描述矩形顶点的运动?如何描述点A?如何描述点B?
 变式:如图,已知⊙O是一根原木的直截面图.现要将该原木加工成直
变式:如图,已知⊙O是一根原木的直截面图.现要将该原木加工成直
截面是矩形的方木,问:怎样设计才能尽量减少木材的浪费.
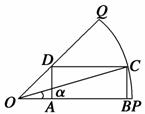 例4 如图所示,已知OPQ是半径为1,圆心角为
例4 如图所示,已知OPQ是半径为1,圆心角为![]() 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
几个三角恒等式
sinacosb=![]() [sin(a+b)+sin(a-b)], cosasinb=
[sin(a+b)+sin(a-b)], cosasinb=![]() [sin(a+b)-sin(a-b)],
[sin(a+b)-sin(a-b)],
cosacosb=![]() [cos(a+b)+cos(a-b)], sinasinb=-
[cos(a+b)+cos(a-b)], sinasinb=-![]() [cos(a+b)-cos(a-b)].
[cos(a+b)-cos(a-b)].
上述表达式把三角函数的乘积化为同名的三角函数的和或者差,统称积化和差公式.
sinA+sinB=2sin![]() cos
cos![]() , sinA-sinB=2cos
, sinA-sinB=2cos![]() sin
sin![]() ,
,
cosA+cosB=2 cos![]() cos
cos![]() , cosA-cosB=-2sin
, cosA-cosB=-2sin![]() sin
sin![]() .
.
上述表达式把同名的三角函数的和或者差化为三角函数的乘积,统称和差化积公式.
第二周选修课:吴祥华老师——三角恒等变换
王友伟老师——不等式,从品老师——数论