
用DIS系统验证玻意耳定律的误差分析
南京市金陵中学 210005 崔卫国

在进行等温定律的实验时,传统的器材操作繁琐,测量步骤较多,实验数据误差较大,常常不能确信产生误差的原因所在。DIS实验系统的出现给中学物理实验带来革命性的改变,在进行气体实验定律的探究或验证时,先进的测量仪器便成为首选。在一次研究等温条件下气体的压强随体积变化的关系时,我们采用了现代化的测量仪器——压强传感器来采集实验数据,期望计算机拟合的图线p—1/V是过原点的直线。可是,事与愿违!拟合的图线p—1/V不是过原点的直线,却总是存在一定的偏离!这是什么原因造成的呢?
下面是学生采集的一次实验原始数据。
如图1,将针筒与传感器连接,缓慢改变气体的体积,进行的数据采集如表1。
表1:环境温度:17.10C
| 计算表格 | 气体压强p/kPa | 活塞对应的刻度—体积:V/cm3 | 体积的倒数:1/V | 压强与体积的乘积:pV |
V'=V+1 |
1/ V' |
| 1 | 105.4 | 16.0 | 0.0625 | 1686.4 |
|
|
| 2 | 112.0 | 15.0 | 0.0667 | 1680.0 |
|
|
| 3 | 119.3 | 14.0 | 0.0714 | 1670.2 |
|
|
| 4 | 127.7 | 13.0 | 0.0769 | 1660.1 |
|
|
| 5 | 137.7 | 12.0 | 0.0833 | 1652.4 |
|
|
| 6 | 148.7 | 11.0 | 0.0909 | 1635.7 |
|
|
| 7 | 162.3 | 10.0 | 0.1000 | 1623.0 |
|
|
| 8 | 178.7 | 9.0 | 0.1111 | 1608.3 |
|
|
| 9 | 198.6 | 8.0 | 0.125 | 1588.8 |
|
|
| 10 | 222.8 | 7.0 | 0.1429 | 1559.6 |
|
|
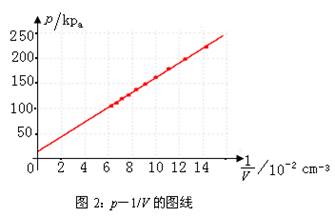
粗略地看,温度不变、质量一定的气体压强与体积的乘积为定值,而且拟合的p--1/V的图线也接近通过原点(如图2),似乎玻意耳定律已经成功地得出。但仔细分析,却有如下问题。
问题1:观察数据,发现温度不变时pV乘积总是随体积的减小而有微小减少,这并不是偶然误差的数据特征,这是为什么呢?
问题2:p-1/V的图线并未通过原点,尽管很接近原点,但绝大多学生得出的图线都出现的是正截距,这又是为什么呢?
学生之间热烈讨论,并提出:(1)可能是活塞与筒壁间漏气?(2)有可能是大家都少考虑了或都多考虑某一引起误差的因素。
从数据看有道理,活塞与筒壁间漏气似乎存在可能。但活塞是双层,且有油密封,压强并不足够大,不应当出现漏气的现象。简短的理性分析后,接着的是短暂的沉默,学生之间的再次实验并相互交流,真的是少考虑了什么物理量吗?
多次实验后终于发现:气体压强的实验数据是精确的,活塞对应的刻度也是准确的,问题出现在测量的实际气体的体积只考虑了针筒内的气体,而传感器管道部分的少量气体却忽略了!
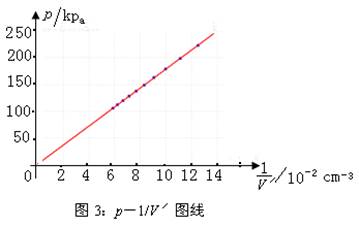
这部分气体经过测算,约有1cm3。若在上表中增加 “V'=V+1”一列作为真正的实际气体的体积,则计算出乘积p V':1791.8,1792.0,1789.5,1787.8,1790.1,1784.4,1785.3,1787.0,1787.4,1782.4。这一组数据非常接近,很好地反映了DIS实验的精确测量!再作出p-1/ V' 的图线(如图3),过原点!这才是最令人兴奋的结果,玻意耳定律终于得到非常确切的验证!
然而,刚才提出的问题并没有彻底解决,图2中正截距的出现,又是什么原因造成的呢?
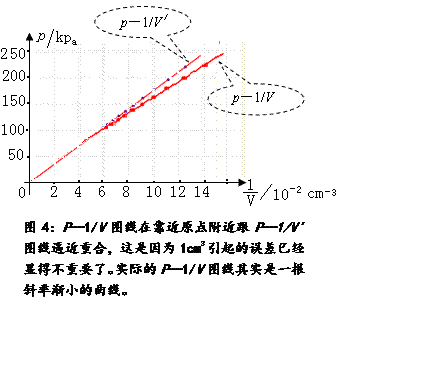
事实上,我们在拟合这些点并寻求规律时,心中期望它是过原点的直线。如果是传统实验仪器的测量而获得的这根不过原点的直线,我们可能不会怀疑什么,可以认为在误差的范围内。而我们现在使用的是精密的传感器测量仪器,出现了令人怀疑的“较大的误差”!仔细观察,这些数据中气体体积较小的部分显得较多,当气体体积被压缩至20~7cm3以下时,因少计入的1cm3引起的误差已经显得特别显著,相对误差在5%~14%,而这部分数据正成为目前拟合的主要依据,于是就出现了不过原点而出现正的截距的直线。当我们将气体体积在20cm3以上的压强也多采集几组数据,结果就不同了。如图4,P—1/V图线在靠近原点附近跟P—1/V' 图线逼近重合,这是因为1cm3引起的误差已经显得不重要了。实际的P—1/V图线其实是一根斜率渐小的曲线。
可见,测量数据分布不够广而进行数据拟合后的非正确图线,以及少计入的1cm3的气体带来的“误差”都是测量考虑不周造成的!
正是因为相信现代化测量仪器的精密,才细细推敲1cm3的气体带来的“误差”,这种怀疑下的探究是可贵而又有意义的。开普勒不就是从怀疑8′的误差而最终成为宇宙的立法者吗!