“探究法拉第电磁感应定律实验”的另种创新设计
南京市金陵中学 江苏 南京 210005 崔卫国
摘要：为了定量探究法拉第电磁感应定律，本文介绍了一组原创性探究实验。该自主设计的实验装置简单，操作方便，测量精确，为物理实验教学的原创设计拓展了思路。
关键词：定律定量测量 原创设计 对称性
在高中阶段，法拉第电磁感应定律是教学实施中“难啃的骨头”。教师往往从定性的角度演示一些较为直观的实验，可以形象地说明匝数越多，磁通量的变化越快，产生的电动势就会越大。但如何精确地探究法拉第电磁感应定律？或如何精确地验证法拉第电磁感应定律呢？这一直是我的心中的念想。前些时日发现《物理教学》杂志2012年第5期介绍的DIS实验能够解决定量探究法拉第电磁感应定律，但该装置结构上较为复杂，操作上需要一定的技巧。该实验能否更加简洁而效果仍然显著？本人经过若干次的设计、试验、检测和改进，终于制作成一组简单可行，可以精确探究的实验装置。
1．电动势与匝数成正比的实验
实验材料：透明PVC管，柱形强磁铁，漆包线，DIS电压传感器，刻度尺。
原创设计：将漆包线绕在透明PVC管上，形成50匝线圈，100匝线圈，200匝线圈，这几组线圈距离管口的位置可以在管壁上任意调整。现将透明管竖直固定，n匝线圈套在距管口距离为h处，线圈两端接DIS电压传感器，如图1。这个实验装置简单，操作方便，实验数据采集精确快捷。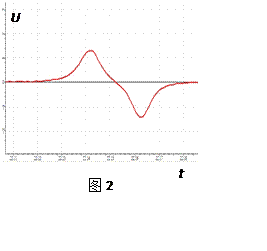
实验过程：现将圆柱形强磁铁从管口自由释放，做自由落体运动的磁铁经过线圈时，借助电压传感器的测量得到了U-t图线，如图2。分别测量50匝，100匝，200匝线圈距管口h=20cm处的正向最大电压峰值，记入表Ⅰ。
表Ⅰ：
| 匝数 n | 下落距离 h/ cm | 最大值 Umax/V |
| 50 | 20.0 | 0.032 |
| 100 | 20.0 | 0.065 |
| 200 | 20.0 | 1.280 |
数据分析：磁铁每一次从同一高度自由下落，在线圈附近同等空间内经历的时间总是相等的，也就是说每一次经过线圈的磁通量的变化快慢总是是相等的。从表格中的数据可以看出，感应电动势的最大值之比为0.032∶0.065∶1.280，与线圈的匝数比1∶2∶4几乎完全一致。虽然数据量偏少，但能够说明：磁通量的变化率相同，电动势与线圈匝数成正比，即
。
2．感应电动势与时间成反比的实验
原创设计：我们取上述同样的自制装置，线圈的匝数恒为n=200匝，并控制线圈距管口有不同的精确距离h，每次让柱形强磁铁从透明管口自由下落。通过电压传感器采集了如下表Ⅱ中若干数据。
表Ⅱ：
| 匝数 n | 下落距离 h/cm | 正向峰值 Umax/V | U-t积分值 |
| 200 | 5.0 | 0.927 | 0.01509 |
| 200 | 10.0 | 1.320 | 0.01524 |
| 200 | 15.0 | 1.582 | 0.01517 |
| 200 | 20.0 | 1.865 | 0.01501 |
| 200 | 25.0 | 2.029 | 0.01511 |
| 200 | 30.0 | 2.160 | 0.01501 |
| 200 | 35.0 | 2.367 | 0.01503 |
| 200 | 40.0 | 2.531 | 0.01505 |
（1）峰值的研究
实验现象：在匝数n相同的情况下，磁铁自由下落的距离h越大，线圈显示出的瞬时电压的最大值也越大。
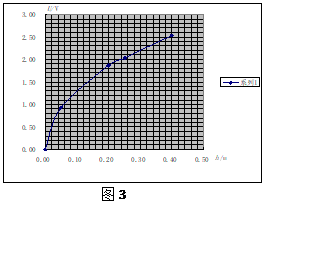
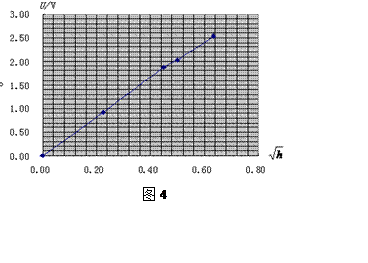
数据分析：我们尝试使用U-h图线初步观察两者的规律，如图3。显然，感应电动势的最大值U与h不成正比例，从图线的走势特点看，我们做了U-
图线，如图4。发现
，为过原点的直线！
如何从理论的角度作出合理的解释呢？
①“切割”的解释：磁铁自由下落到线圈处的速度为
，即线圈切割磁场的速度与下落距离的平方根成正比。图线中的规律
反映了线圈中产生的电动势与切割磁场的速度成正比。若令此磁极经过线圈处的有效切割磁感应强度为B，则动生电动势U=BLv切在此可以得到验证。
”，在⊿y较小的情况下，v可以表示为。于是，从上面的图线，我们可以有这样的推断：在线圈匝数相等的条件下，感应电动势的大小E与时间⊿t成反比，即
。（2）U-t图线积分值的研究
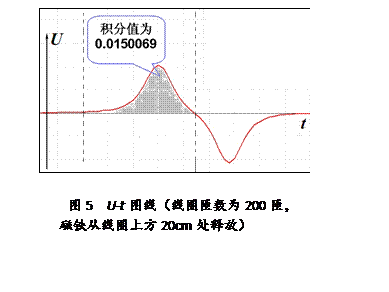
实验现象：柱形磁铁通过线圈后，电压传感器采集到的U-t图线记录如图5。磁铁下落不等的距离h，U-t图线的形状相似，但峰值随下落距离的增大而增大。经过仔细的观察，表格中还发现这几个U-t图线有着这样的共同特征：正向最大电压值越大的曲线与时间轴相交的时间间隔就越小，虚线间U-t图线覆盖的面积总是相等！（即表格中的U-t积分值近似相等）
这又如何解释呢？
由于磁铁的外径比线圈的内径稍小，因此从磁铁接近线圈到经过线圈的过程看，左虚线为磁铁通过线圈的磁通量从零（极少）开始变多的临界点。从对称的角度看，右虚线对应柱形磁铁的中间部位经过线圈的临界点，此时线圈中磁通量最大为Фmax。换言之，两根虚线代表了线圈中从零到最多磁通量Фmax的变化，无论磁铁从何种不同的高度自由下落，这两个线代表的时间间隔(Δt)可以不等，但这段时间内的磁通量的变化(ΔФ)确实是相等的。
显然，两根虚线相对于线圈所表示的磁通量（0→Фmax）的空间变化并不因下落高度的不同而改变，只是下落的高度越高，发生相同磁通量的变化(ΔФ)所需的时间(Δt)就越短。难道“磁通量的变化(ΔФ)与所需的时间(Δt)成反比吗？”
我们不断改变磁铁下落的高度，测得的数据如表中所示。下落的任意性或Δt值的不同性总是不改变“U-t图线覆盖的面积总是相等”这一结论！从微积分的角度看，我们只能做出一个大胆的推断：在相同磁通量变化的情形下，产生的电动势与相应的时间的乘积为一个定值。结论便显然于眼前：在匝数相等，磁通量变化相同的条件下，电动势与时间成反比！即
。
3．电动势与磁通量变化成正比的研究
实验材料：方形强磁铁（5cm×5cm×2cm，如图6），漆包线，DIS电压传感器。
原创设计：“品”形线圈，a、b线圈各自独立，匝数均为50匝，用胶密封，其中a线圈的面积是4cm2，b线圈面积的12cm2，如图7。
实验过程：如图8，将“品”形线圈平放于水平桌面，让方形磁铁从线圈的正上方落下，使用两个电压传感器同时测量不同面积线圈的输出电压U1和U2。图9中峰值为0.10V的图线是在面积为4cm2的a线圈两端采集的；峰值约为0.30V的图线是在面积为12cm2的b线圈两端采集的。
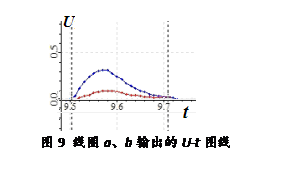数据分析：当方形磁铁下落到线圈上方附近时，线圈中产生了感应电动势，从图线看，不但是电压的峰值之比是1∶3，几乎每时每刻的电压值之比都是1∶3。由于方形磁铁下方穿过“品”形线圈的磁场具有对称性，即使线圈中的磁场在变化，但每时每刻的磁场强弱的变化率时刻一致，则通过线圈的磁通量的变化与面积就成正比，即1∶3。可见，这组数据反映了：在相同的时间内电动势与磁通量的变化成正比的规律，即
。
另一种设计方案：
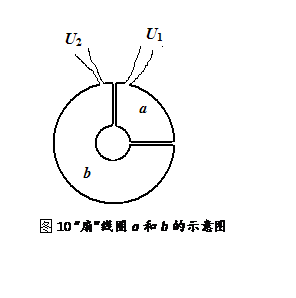
原创设计：如图10，a、b两个独立的扇形线圈，匝数均为50匝，面积之比1∶3，并用明胶胶合在同一平面，如图10。
实验过程：将该a、b扇形线圈垂直套在透明管上，如图。让圆柱形强磁铁从一定的高处释放，磁铁在管中自由下落通过线圈，用DIS电压传感器分别测出获得的感应电动势即线圈的输出电压U1和U2。实验表明，输出电压的最大值显示出1∶3的关系。
数据分析：由于圆柱形磁铁周围磁场具有高度的对称性，a、b扇形线圈的设计也正是利用了这种对称性的特点。当磁场穿过扇形线圈时，相同时间内a、b扇形线圈中发生的磁通量的变化之比就精确表示为1∶3。于是得到同样的结论：在相同的时间内电动势与磁通量的变化成正比的规律，即
。
实验总结：，
。
原创说明：本组器材中透明PVC管和柱形、方形强磁铁易购买。线圈的绕制简单，可动性强，在制作上考虑了柱形磁铁和方形磁铁周围磁场的对称性特点，而且在操作上显得简洁方便，测量上则借助了DIS电压传感器的精确性和快捷性。还需要说明的是，上述采集的数据在磁铁距线圈的距离不太大时更能反映规律上正比或反比，在距离较大时会受到线圈本身对磁铁的运动会产生一定的“阻碍”，得到的数据会向某个固定的方向偏离，属于系统误差。
作者：崔卫国 13585192499
地址：南京市中山路169号 210005
当前位置：